Think of map projections as the clever but imperfect art of flattening the Earth. Since our planet is a curved, three-dimensional sphere (or, more precisely, an oblate spheroid—slightly squashed at the poles and bulging at the equator/‘Geoid’), displaying it on a flat map, like a piece of paper or a screen, is a real challenge.
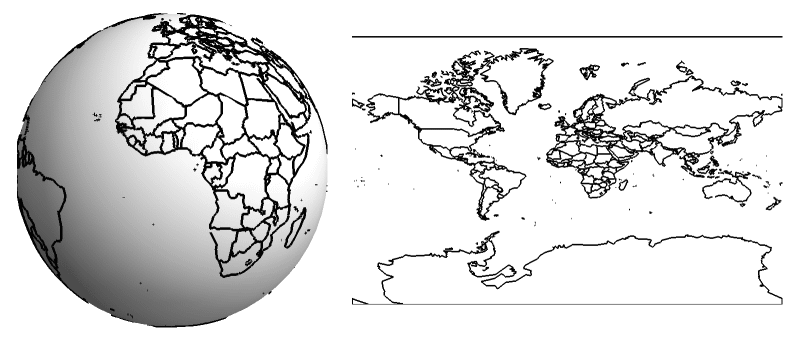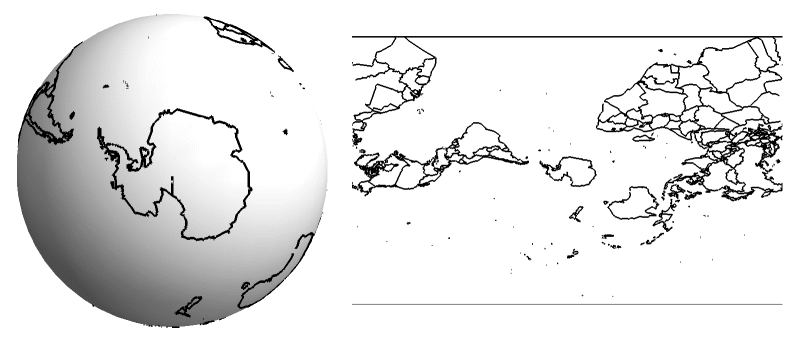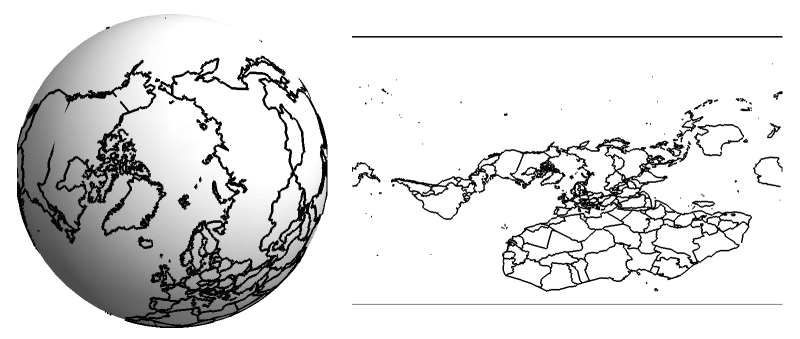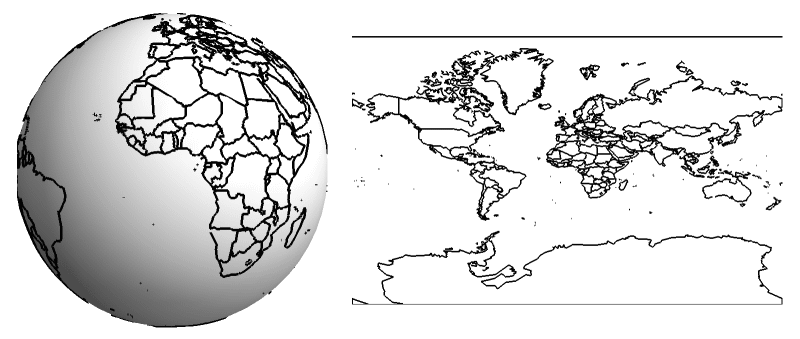
Distortion in Maps
The core problem is simple: you can’t perfectly flatten a curved surface without stretching, tearing, or squishing parts of it. Imagine trying to smooth out an orange peel without tearing it—it’s impossible! This means that every single map projection will introduce some kind of distortion.
Cartographers, the experts who make maps, have to make a tough choice. Since map projections are mathematical methods that translate the Earth’s curved coordinates onto a flat surface. This “translation” always involves trade-offs, making the cartographer’s job about intelligently deciding which geographical properties are most crucial to preserve for a map’s specific purpose. They can’t preserve all of the Earth’s geographical properties accurately at the same time. These properties include:
- Direction: True bearings and angles.
- Area: The true relative sizes of landmasses.
- Shape: The correct outlines and forms of features.
- Distance: Accurate measurements between points.
Why Map Projections Are Essential
Given this fundamental limitation, why bother with map projections at all? Because flat maps are incredibly useful! They’re portable, easy to store, and simple to measure on. The trick lies in strategic compromise. A cartographer chooses a specific projection based on what the map will be used for.
For instance:
- A navigation map (like those used for sailing or flying) prioritises accurate directions and angles, even if it means landmasses appear stretched or shrunken in certain areas.
- A thematic map showing population density or climate zones, however, needs to maintain the correct relative sizes of countries and continents so that comparisons are accurate, even if their shapes get a bit distorted.
A sphere is not a developable surface but is the closest geometrical form to the shape of the Earth, i.e., the Geoid. The shapes that form a developable surface are 2-dimensional geometric shapes like the Cone, Cylinder and Circle.
When we construct maps, we try to represent four geographical characteristics: Area, Shape, Bearing, and Distance. There can also be a fifth type in which none of the above features are preserved.
Classification based on preservation :
Based on certain attributes, the following types of projections can be made…
| Preservation | Projections |
| of area | Equal Area or Homolographic Projection |
| of shape | Orthomorphic Projection |
| of bearing | Azimuthal Projection |
| of distance | Equidistant Projection |
| none | Aphylactic Projection |
Classification based on Development :
Perspective Map Projections
Map projections are techniques used to represent the three-dimensional Earth’s surface on a two-dimensional plane. These projections can be categorised based on three main factors: the type of developable surface used, the viewpoint or perspective, and the projection aspect.
Types of Surfaces:
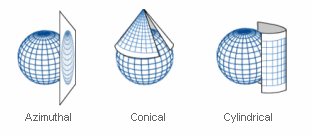
- Cylinder: The Earth’s surface is projected onto a cylinder that touches the globe along a central meridian or equator.
- Cone: The surface is projected onto a cone that intersects the globe along one or two parallels (lines of latitude).
- Plane: The projection is made onto a plane that tangents or cuts through the Earth’s surface at a specific point or along a line.
Viewpoints or Perspectives:
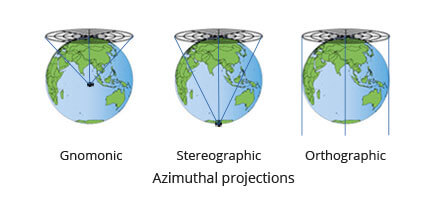
- Center (Gnomonic Projection): The light source is directly above the surface’s centre, creating accurate angles but highly distorted distances and areas.
- Periphery or Antipodal (Stereographic Projection): The light source is located at the surface’s opposite pole, resulting in conformal projections that preserve angles but distort shapes and areas.
- Infinity (Orthographic Projection): The light source is infinitely far away, producing equal-angle projections that maintain the correct appearance of angles and shapes but distort sizes and distances.
Projection Aspects:
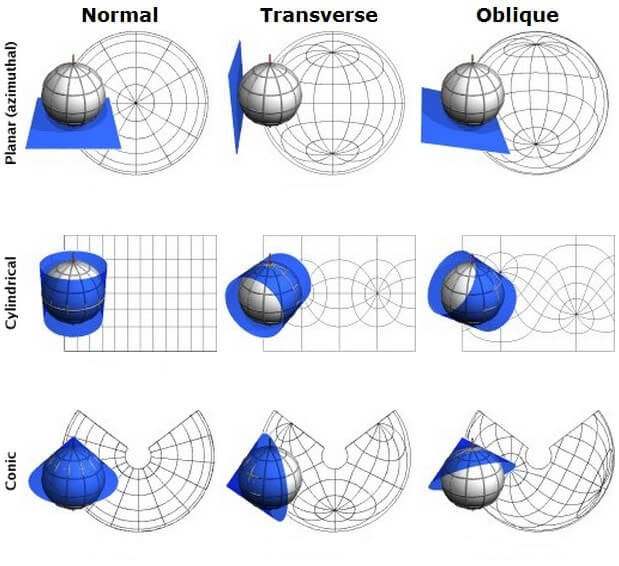
- Polar: The central meridian of the projection passes through one of the Earth’s poles.
- Equatorial (or Transverse): The central meridian is the Earth’s equator, or, in the case of a transverse projection, a meridian 90 degrees from the equator.
- Oblique: The central meridian is neither through a pole nor the equator, slanting across the globe to best represent a specific region.
Non-Perspective Map Projections
Non-perspective map projections, also known as mathematical or analytical projections, do not simulate projecting the Earth’s surface onto a developable surface (like a cylinder, cone, or plane) from a specific viewpoint. Instead, they use mathematical formulas to transform geographic coordinates (latitude and longitude) into planar coordinates (x and y). These projections are commonly used when exact geometric accuracy isn’t the main priority, and they can be categorised based on the property they prioritise most:
- Conformal Projections: These projections preserve local angles, meaning that small shapes retain their true angles and form, though area and distance can be distorted. Examples include the Lambert Conformal Conic projection and the Stereographic projection when used in a non-perspective sense. Although the Mercator projection is technically a perspective cylindrical projection, it is often discussed with conformal projections because of its ability to preserve angles.
- Equal-Area (or Equi-Area) Projections: These projections ensure that the relative areas of regions are maintained, though their shapes and angles might be distorted. Examples include the Albers Equal-Area Conic projection, the Lambert Azimuthal Equal-Area projection, and the Mollweide projection.
- Equidistant Projections: These preserve true distances along specific lines (typically the central meridian or the equator) or between certain points. Elsewhere, distances, angles, and shapes may be distorted. Examples include the Equirectangular projection and the Central Cylindrical projection. The Robinson projection, while primarily a compromise projection, also maintains some equidistant properties.
- Compromise Projections: These aim to balance the preservation of angles, areas, and distances, without perfectly preserving any of them. The Robinson projection is a well-known example, designed for aesthetic purposes, while others like the Winkel Tripel and Van der Grinten projections similarly seek a balanced view.
Non-perspective projections are selected based on the map’s intended purpose, often prioritising area, shape, or distance depending on the region being mapped. This makes them especially useful for various applications, including global or regional maps, where distortion trade-offs are necessary.