The Sanson-Flamsteed Projection, also known as the Sinusoidal Projection, is one of the earliest equal-area projections used in cartography. It was independently developed by two individuals: Nicolas Sanson (a French cartographer) in the 17th century and John Flamsteed (the first Astronomer Royal of England) in the 18th century.
Why is it known as a Sinusoidal Projection?
The Sanson-Flamsteed Projection is called Sinusoidal because the shapes of the meridians (except the central meridian) follow a curve that resembles a sine wave.
The Sanson-Flamsteed Projection is called Sinusoidal because the shapes of the meridians (except the central meridian) follow a curve that resembles a sine wave. This mathematical property ensures that the projection maintains equal-area representation.
Mathematical Explanation:
In the Sinusoidal Projection, the horizontal distance (x) of a point from the central meridian is proportional to the longitude and the cosine of the latitude. This means that the shape of each meridian, except the central one, follows a path similar to a sine wave.
The formula for the (x)-coordinate in a sinusoidal projection is:
$$x = R \, \lambda \, \cos \phi$$
$$Where: (x) = horizontal coordinate; (R) = radius of the Earth; (\lambda) = longitude of the point from the central meridian; (\phi) = latitude of the point$$
The central meridian is a straight line, but the other meridians curve in a way that resembles the periodic wave pattern of a sine function (hence the name sinusoidal).
Visual Explanation:
Just like a sine wave fluctuates symmetrically around a central axis, the meridians in a sinusoidal projection curve symmetrically to the left and right of the central meridian, depending on how far from it they are. The projection ensures that the area between the meridians and parallels is accurate, even though shapes may get distorted.
The curved meridians that mimic a sine-like path are a defining characteristic. The name reflects how mathematical cosine functions (derived from the sine function) govern the projection’s geometry to preserve areas accurately.
Construction:
Question: Construct a Sinusoidal Projection at a scale of 1:250,000,000 at 30° intervals.
Solution:
To find the radius of the Earth on the map based on the scale 1:250,000,000, we can use the following steps:
- Radius of the Earth: The Earth’s actual radius is approximately 6,371 km (or 6,371,000 meters).
- Map Scale: The scale of 1:250,000,000 means that 1 unit on the map represents 250,000,000 units on the Earth’s surface.
- Converting to centimetres:
- The Earth’s radius in centimetres is 6,371,000,000 cm (since 1 km = 100,000 cm).
- Now, divide this by the scale factor 250,000,000 to get the radius on the map.
$$\text{Radius on map (in cm)} = \frac{6,371,000,000}{250,000,000}$$
Radius = 2.55 cm
4. Distance between the meridian can be found out by finding the length of the arc subtended by 30° on a circle with the radius
$$\text{Arc Length} = 2\pi r \times \frac{30^\circ}{360^\circ}$$
$$\text{Arc Length} = 2\pi \times 2.55 \, \text{cm} \times \frac{30}{360}$$
$$\text{Arc Length} \approx 1.336 \, \text{cm}$$
5. Length of equator: $$\text{Circumference} = 2 \pi r$$
Length of Equator = 16.01 cm
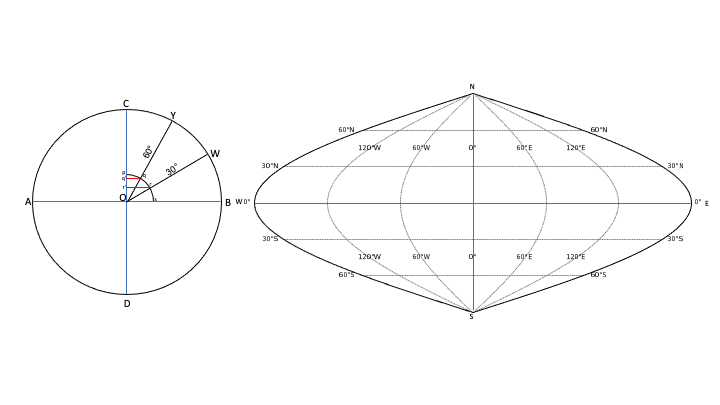
- Draw a circle with a radius of 2.55 cm from point O
- From point O make diameter AB
- CD intersects AB at O at 90°
- From point, O draws OW and OY at 30° and 60° respectively
- Draw an arc pqrs with the length of arc 1.336 cm from point O
- Drop perpendicular rr’ and qq’ from where the arc pqrs intersects OW and OY
- Draw the projection:
- Draw line WE representing 0° of length 16.01 cm.
- Divide WE into 6 equal parts at 60° intervals (360°/30°)
- NS is the central meridian bisecting WE from the centre. Its length is half of the equator (16.01/2=8 cm).
- NS is also bisected by WE.
- Divide NS into 3 equal parts on either side of WE
- Os, rr’ and qq’ is the distance between the meridians on latitudes 0°, 30° and 60° respectively
