Object. To study the temperature dependence of total radiation and to verify the Stefan’s law.
Apparatus Required. 6 V battery, key, DC voltmeter of range 0-10 V, DC ammeter of range 0-1 A, electrical bulb of tungsten filament of rating 6 V, 6 W, rheostat of resistance 100Ω and connection wires.
Theory. According to Stefan’s law, the total radiation emissivity of a black body (i.e., the total radiant energy emitted per unit area per second by a black body) is directly proportional to the fourth power of absolute temperature T of that body, i.e.,
E ∝ T4 or E = σ T4 ……………. (1)
where σ is Stefan’s constant.
Now if the tungsten filament of the electric bulb is assumed to be the black body, according to Stefan’s law, the total radiant power emitted by it is
P ∝ Tα or P = CTα
Taking logarithm on both sides,
log10P = log10C +α log10T ………………(2)
Hence a graph plotted between log10P versus log10T will be a straight line with slope α (= nearly 4).
The temperature of filament of bulb is determined by measuring its resistance. The variation of its resistance with temperature is given by the following relation:
Rt = R0 (1 + αt + βt2) ………………………(3)
where R0 = resistance of filament at 0°C, Rt = resistance of filament at 1°C and α and β are the temperature coefficients of resistance.
For the tungsten filament, α = 5.21 x 10-3 °C-1 and β = 7.2 * 10-7 °C-2, hence assuming the temperature of filament at just glow to be 530°C, the value of the quantity 1 + αt + βt2 comes out to be 3.96. Then,
R0 = Rg /3.96 …………………………….. (4)
where Rg is the resistance of filament at just glow.
From Ohm’s law,
Rg = Vg / Ig …………………………………(5)
where Vg and Ig are respectively the voltage applied across the ends of the bulb and the current flowing in it, at just glow of its filament.
Thus, knowing Rg the value of R0 can be calculated. Then the resistance Rt of the filament of bulb is measured by finding the ratio of voltage and current, at any temperature t. After this, the value of Rt / R0 is calculated and then from the calibration curve plotted for Rt / R0 versus t for the tungsten filament, the temperature t of the filament corresponding to that value of Rt / R0 is obtained.
Formula used. The resistance of filament of bulb at any temperature t is Rt =V/I where V is the potential difference applied across the filament of the bulb and I is the current flowing in the filament.
Resistance of filament of bulb at just glow Rg = Vg / Ig,
where Vg is the potential difference applied across the filament and Ig is the current flowing in the filament, when it just glows.
Resistance of filament of bulb at 0°C is R0 = Rg / 3.06
According to Stefan’s law, if the absolute temperature of filament of bulb is T, the total radiant power P emitted by it is given as
log10P = log10C +α log10T
Hence a graph plotted between log10P versus log10T will be a straight line with slope α (= nearly 4).
Procedure. (Not to be written in copy)
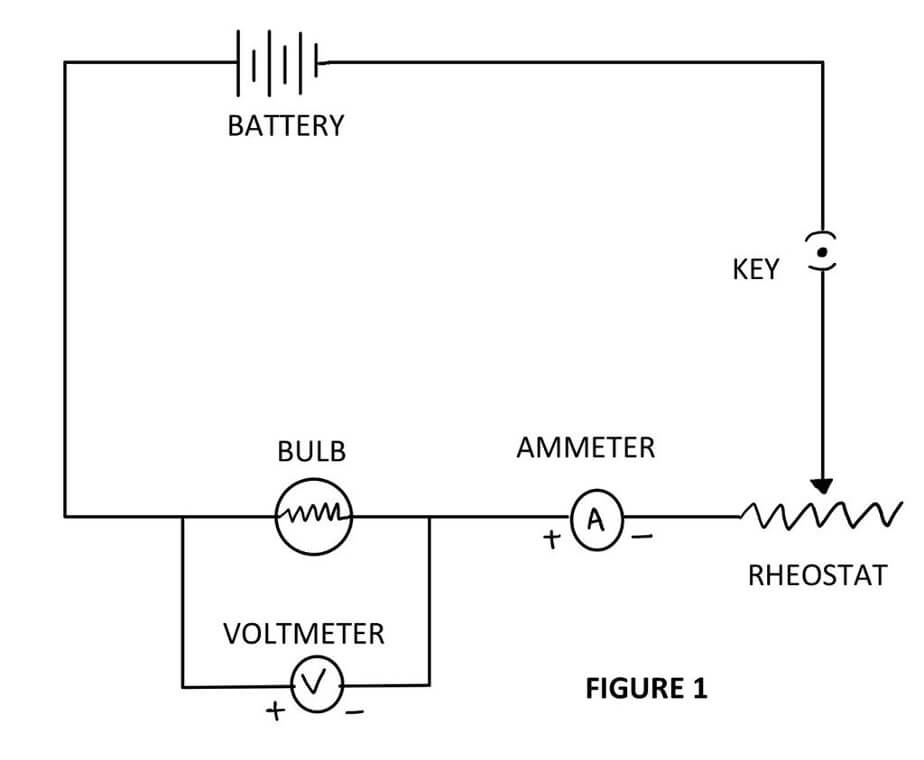
First, the circuit is connected as shown in Fig. 1. For this, a battery, rheostat, key and ammeter are connected in series with the bulb and a voltmeter is connected in parallel across the bulb. Take care that the +ve marked terminals of ammeter and volt-meter are connected with the +ve terminal of the battery and no holder is used with the bulb, otherwise additional resistance will get added with the filament of bulb. Hence at the base of the bulb, its terminals are soldered at two different points with the wires.
Now the experiment is performed in the following two parts:
- To find the resistance of filament of bulb at 0°C,
- To find the absolute temperature (in kelvin) of the filament of bulb and the total radiant power emitted by it.
(i) To find the resistance of filament of bulb at 0°C
1. By inserting the plug in the key, the rheostat is adjusted to its maximum value so that a very feeble current flows in the bulb. Then the sliding terminal of the rheostat is gradually moved to decrease the resistance till the bulb gets just glow (i.e., the filament appears faint red). In this situation, the reading Ig of ammeter and the reading Vg of voltmeter are noted.
2. Now the resistance of circuit is much decreased so that the bulb glows with white illuminance. Then sliding the variable terminal of the rheostat, the resistance of circuit is increased till the bulb again appears faint red. Again, the reading Ig of ammeter and the reading Vg of voltmeter are noted.
3. Repeat the above steps three times.
4. For each observation, calculate Rg = Vg / Ig and then find the mean value of Rg.
5. Then calculate the resistance R0, of the filament at 0°C using the relation R0 = Rg / 3.96.
(ii) To find the temperature T (in kelvin) of the filament of bulb and the total radiant power emitted by it
1. After inserting the plug in the key, the current in circuit is gradually increased from its low value with the help of rheostat and each time the reading V of voltmeter and the reading I of ammeter are noted. This is done till the bulb illuminates with white glow.
2. For each observation, Rt = is calculated and then Rt / R0 is determined.
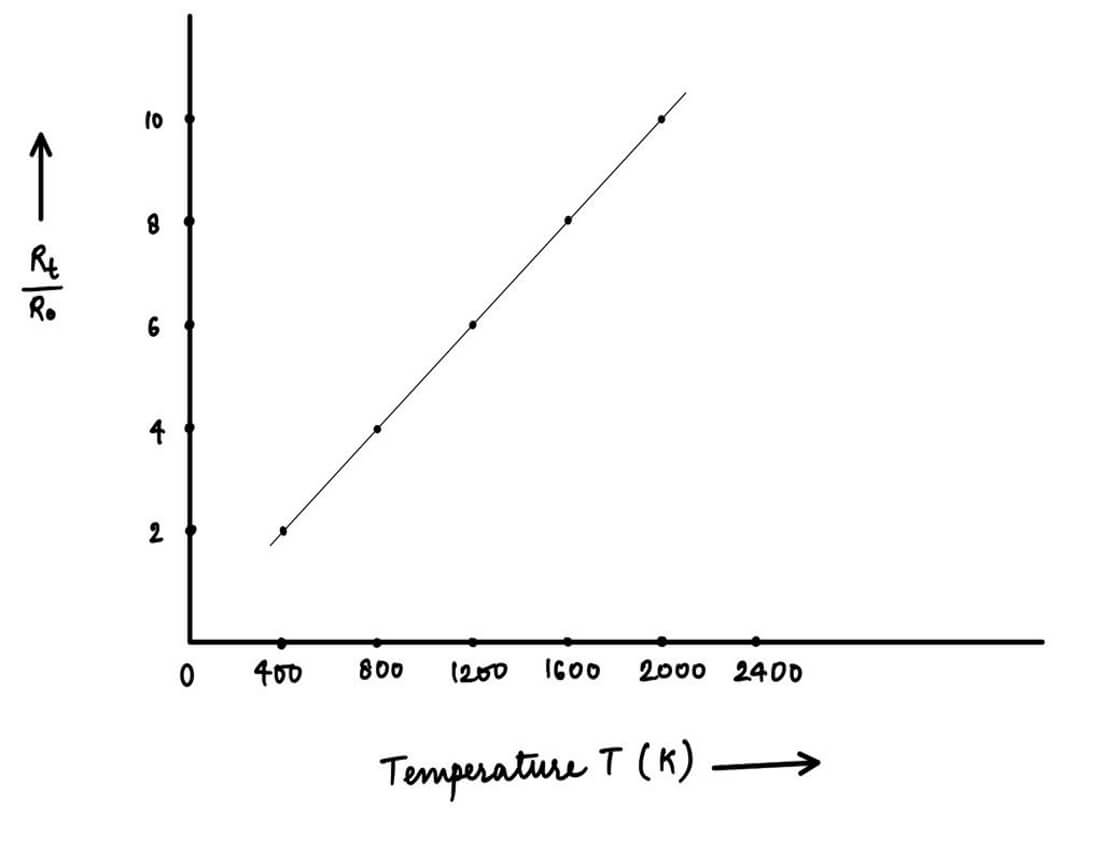
3. For each value of Rt / R0, either from the calibration curve given in Fig. 2 (or from the table given below), the temperature T of the filament of bulb (in kelvin) is determined.
| Temperature T (K) | Rt / R0 | Temperature T (K) | Rt / R0 |
| 273 | 1.00 | 1273 | 6.94 |
| 373 | 1.53 | 1373 | 7.60 |
| 473 | 2.07 | 1473 | 8.26 |
| 573 | 2.13 | 1573 | 8.90 |
| 673 | 3.22 | 1673 | 9.70 |
| 773 | 3.80 | 1773 | 10.43 |
| 873 | 4.40 | 1873 | 11.17 |
| 973 | 5.00 | 1973 | 11.42 |
| 1073 | 5.64 | 2073 | 12.69 |
| 1173 | 6.37 | 2173 | 13.50 |
Table: Values of Rt / R0 at different temperatures for the tungsten filament
4. For each observation, calculate power P radiated by the filament using the formula P = VI. Then find log10P and log10T. Now plot a graph by taking log10P on Y-axis and log10T on X-axis which comes out to be a straight line. The slope of the line is determined.
Observations.
- For finding the resistance R0 of filament of bulb at 0°C.
Least count of Voltmeter = …………………… V
Least count of Ammeter = ……………………. mA
| S. No. | While increasing current | While decreasing current | ||||
| Voltmeter reading Vg (V) | Ammeter reading Ig (mA) | Resistance at just glow Rg=Vg/Ig (Ω) | Voltmeter reading Vg (V) | Ammeter reading Ig (mA) | Resistance at just glow Rg=Vg/Ig (Ω) | |
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
Mean Rg = …………. Ω
R0 = Rg / 3.96 =………………. Ω
- For finding the temperature T (in kelvin) of the filament of bulb and the total radiant power emitted by it.
| S. No. | Voltmeter reading V (V) | Ammeter reading I (mA) | Resistance Rt=V/I (Ω) | Rt / R0 | Temperature of filament T from calibration curve/ table (K) | Power radiated P=VI (W) | log10T | log10P |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. |
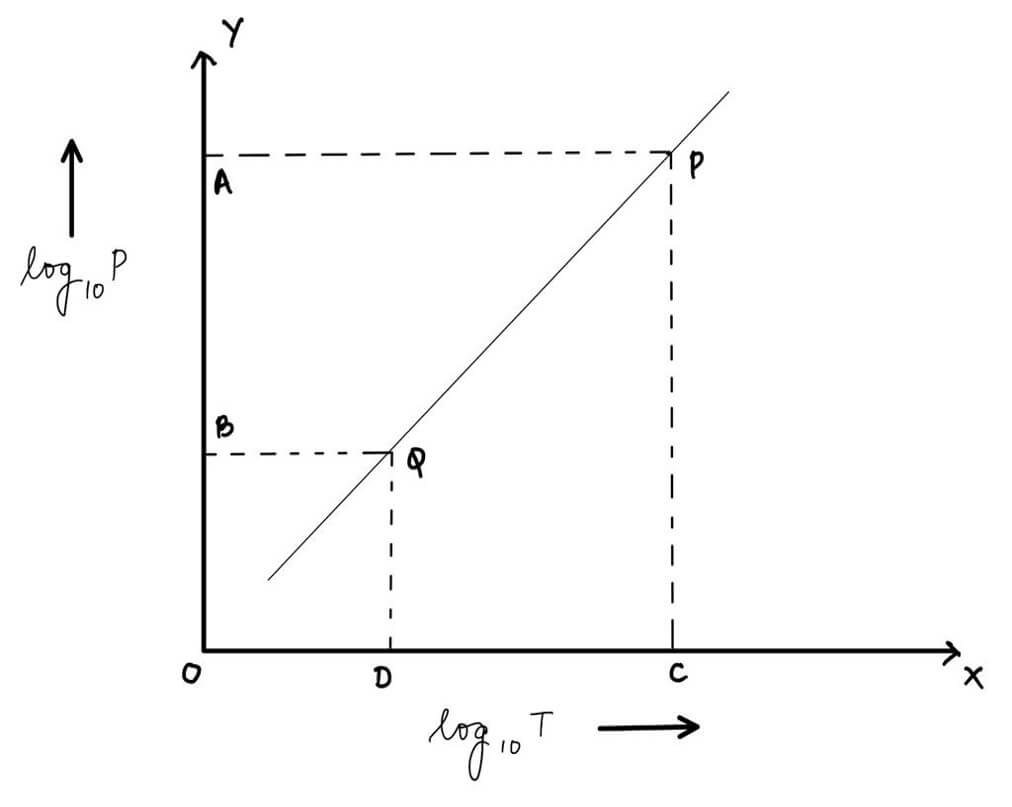
Calculations. Slope of the straight line is obtained from the graph plotted with the above tables between log10P and log10T. The slope is
s= log10P / log10T
Result. The graph plotted between log10P and log10T is a straight line as shown in fig. 3, hence it verifies the relation P = CTα. Moreover, the slope of the straight-line s = 4 (nearly), hence it verifies the Stefan’s law.
Precautions.
1. The bulb should not be fixed in the holder, otherwise an additional resistance of the holder comes in the circuit.
2. The readings of voltmeter and ammeter while measuring the resistance of filament at just glow should be noted only when the filament of the bulb appears to be faint red.
Viva- Voce
Q. What is Stefan’s Law?
Ans. According to Stefan’s law, the total radiation emissivity of a black body (i.e., the total radiant energy emitted per unit area per second by a black body) is directly proportional to the fourth power of absolute temperature T of that body, i.e., E ∝ T4 or E = σ T4 where is called the Stefan’s constant.
Q. What do you mean by perfectly black body?
Ans. A body which absorbs whole of the radiant energy incident on it, is called the perfectly black body.
Q. What is the perfectly black body in your experiment?
Ans. The filament of the tungsten bulb.
Q. What do you mean by emissivity of a surface?
Ans. The total amount of energy emitted per second by the unit area of a surface is called its emissivity.
Q. On what factors does the amount of energy emitted from a surface depend?
Ans. The amount of energy emitted from a surface depends on (i) Area of the surface, (ii) absolute temperature of the surface, (iii) time and (iv) nature of the surface.
The energy emitted from a surface = σ T4
where, σ = Stefan’s constant, T = absolute temperature of the surface, A = area of surface, t = time, e = relative emittance of the surface (= emissivity of surface/ emissivity of perfectly black body).
Q. What is the value of e of a perfectly black body?
Ans. 1.
