Object: To use de Sauty’s bridge and compare the ratio of capacitances with the ratio of resistances of the opposite arms.
Apparatus: Two condensers (capacitors), one known resistance, one resistance pot, AC Source, detector and insulated connecting wires
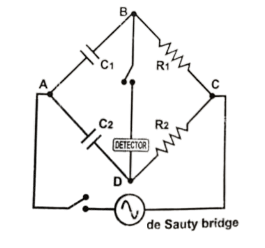
Theory: The de Sauty’s bridge is an AC bridge which works on the principle of Wheatstone’s bridge. This bridge is used to determine the capacity of an unknown capacitor C2 in terms of the capacity of a standard known capacitor C1. Here R1 and R2 are non – inductive resistors. R1, R2, C1 and C2 are connected in a Wheatstone’s bridge as shown in the figure. When the bridge is balanced, the ratios of impedances are equal as given below:
\[
\frac{Z_1}{Z_2} = \frac{Z_3}{Z_4}
\]
\[
\Rightarrow \frac{\frac{1}{j \omega C_1}}{R_1}=\frac{\frac{1}{j \omega C_2}}{R_2}
\]
\[
\Rightarrow \frac{C_1}{C_2} = \frac{R_2}{R_1}
\]
Formula
\[
\frac{C_1}{C_2} = \frac{R_2}{R_1}
\]
where C1 and C2 are the capacitances of the known capacitor. R1 is the fixed resistance and R2 is the variable resistance.
Procedure.
- Connect the circuit on the experimental board as per the circuit diagram shown in the figure.
- Record the values of
C1 = …..μF, C2 = …….μF and R1 = …………..kΩ
- Switch on the power.
- Now vary pot R2, carefully and keep an eye on the voltmeter (VAC (p-p)) so that the voltmeter shows the minimum deflection for a value of R2.
- Caution: Do not disturb the pot R2 for the above setting.
- To measure the value of R2 remove all the connections made for fig (1). Now use the digital multimeter in the proper KΩ range across the pot R2, Record the value of R2
- Calculate the ratio (C1/C2) by the recorded values of C1 and C2 and compare it with the ratio of the opposite arms (R2/R1). Repeat this step at least thrice.
- Repeat steps 1 to 5 with varied values of C1, C2 and R1.
Observations.
| S.No. | Given values | Experimental value (R2 in KΩ) | Mean R2 (kΩ) | Ratio | |||||
| C1 (μF) | C2 (μF) | R2 (KΩ) | R2 (I) | R2(II) | R2(III) | C1/C2 | R2/R1 | ||
| 1. | 0.1 | 0.1 | 1 | ||||||
| 2. | 0.1 | 0.1 | 2 | ||||||
| 3. | 0.1 | 0.047 | 1 | ||||||
| 4. | 0.1 | 0.047 | 2 | ||||||
| 5. | 0.047 | 0.047 | 1 | ||||||
| 6. | 0.047 | 0.047 | 2 | ||||||
| 7. | 0.047 | 0.1 | 1 | ||||||
| 8. | 0.047 | 0.1 | 2 | ||||||
Result.
- The ratio of capacitances with the ratio of resistances of the opposite arms have been compared using de Sauty’s bridge.
- It has been observed that, within the limit of experimental error, the ratio of capacitances is equal to the ratio of the resistances of the opposite arms for all the values of capacitance.
Precautions.
- The connecting wires should not be in contact with the experimental table.
- The wires are checked up for continuity.
- The resistors and capacitors used should be of proper range.
- The multimeter should be set in a proper range.
Viva – Voce
Q. What is a capacitor?
Ans. Capacitor is meant to store electrical energy and release it whenever desired. It is a device in which a large amount of charge can be stored. A capacitor is a pair of two conductors of any shape which are close to each other and have equal and opposite charges.
Q. What do you mean by the capacitance of a capacitor?
Ans. If the charges on the plates of a capacitor +q and -q and the potential difference between them be V, then the capacitance of the capacitor is given by C= q/V. Thus, the capacitance of a capacitor is defined as the ratio of the charge given to a plate of the capacitor to the potential difference produced between the plates.
Q. On what factors the capacity of a capacitor depends?
Ans. It depends upon the following three factors 1. Area of the plate, capacity increases with the increase of area. 2. Distance between the plates, capacity increases when the distance between the plates is decreased. 3. Dielectric constant of the medium, greater the value of the dielectric constant, greater the capacity.
Q. What is the function of the dielectric in the capacitor?
Ans. It increases the capacity of the capacitor.
Q. Define dielectric constant of a material.
Ans. The ratio of the capacitance with and without the dielectric between the plates is called dielectric constant of the material used.
Q. Which is the best dielectric for a capacitor and why?
Ans. Mica is the best dielectric because its dielectric constant is high (6 at 20oC). Its insulation does not break even if high potential difference is applied on its coating. It is used in all good standard capacitor.
Q. Define one farad.
Ans. Capacitance of a capacitor is said to be 1 Farad if one Coulomb of charge raises its potential through 1 volt. The Farad is too large unit ( one farad spherical conductor must have a radius of 9 * 10 9 meter). Hence, in practice, smaller units such as microfarad (μF) and picofarad (pF) are used.
Q. What kind of bridge de Sauty is? AC or DC?
And. It is an AC bridge.
Q. What do you mean by Wheatstone’s bridge?
Ans. In the Wheatstone’s bridge arrangement, four resistances are so connected as to form a parallelogram. In one diagonal of this parallelogram is connected a galvanometer, and in another diagonal a cell. Now, if the resistances in the four arms of the parallelogram are so adjusted that on sending current in the bridge by the cell, there is no deflection in the galvanometer then the bridge is said to be balanced. In this condition, the ratio of the resistances of any two adjacent arms of the bridge is equal to the ratio of the resistances of the remaining two adjacent arms.
Q. How does sensitivity of the Wheatstone’s bridge depend on the values of resistances?
Ans. The sensitivity of the bridge depends upon the values of the resistances. The bridge is maximum sensitive when all the four resistances are of the same order.
Q. What is the limitation of the de Sauty’s bridge?
Ans. De Sauty’s bridge does not provide accurate results for the capacitor which has dielectric losses.
